Information Theory in ML

Information Theory Basis

1. Information and Entrophy

self-info

self-information is a measure related to the outcome of a probabilistic event. To quantify the information, we hope the measure would have following properties:

• A low-probability outcome contains more infomation than a high-probability event. For example, "I won't die" contains more information than "I will die". To some extent, we can regard self-info as the degree we would feel surprise about an certain outcome of an event
• Information quantity must not be negative
• The total imformation of several outcome should be the sum of ther individual information
• \(I(y=m_1,y=m_2) = I(y=m_1)+I(y=m_2)\)
• I(y) must be continuous if P(y) is continuous

It can be proved that the only expression that satisfies these properties is \(Klog(P(y))\) where K is negative. Set K= 1, we define the self-information of an outcome of an event as: \[ I = log(\frac{1}{P(y=c_m)}) = -log(P(y=c_m)) \]

Entrophy

Entrophy is the expectation of self-info. It represent the mean information of an event related to an random variable y, the greater H is, the more uncertain event y is \[ H(Y) = E[I(y)] = -\sum_m^k p(y=c_m)log(p(y=c_m)) \]

2. Entrophy measure for two variables

2.1 Joint Entrophy

Joint entropy measure the uncertainty of a joint event (X, Y) \[ H(T,Y) =-\sum_t\sum_y p(t,y)log(p(t,y)) \]

2.2 Conditional Entrophy

Conditional Entrophy represent the Information recieved of one event when another event is for certain \[ H(Y|T) =-\sum_t\sum_y p(t,y)log(p(y|t)) = -\sum_t\sum_y p(y|t)p(t)log(p(y|t)) \] The higher H(Y|T) is, the less "extra information" about Y is needed when T is certain, which means the corralation between Y and T l is higher

The relationship between conditional entropy and joint entropy: \[ H(Y｜T) = H(Y, T) - H(T) \]

2.3 Inofrmation Gain

Information gain represent the amount of uncertainty reduction of a variable when another variable is certain \[ IG(Y|T) = H(Y) - H(Y| T) \] It is usually applied as an impurity metrics in splitting algorithm like Decision Tree

2.4 Mutual Information

The nature of Mutual Information and Information Gain is the same, mutual information is the shared entropy of two variable

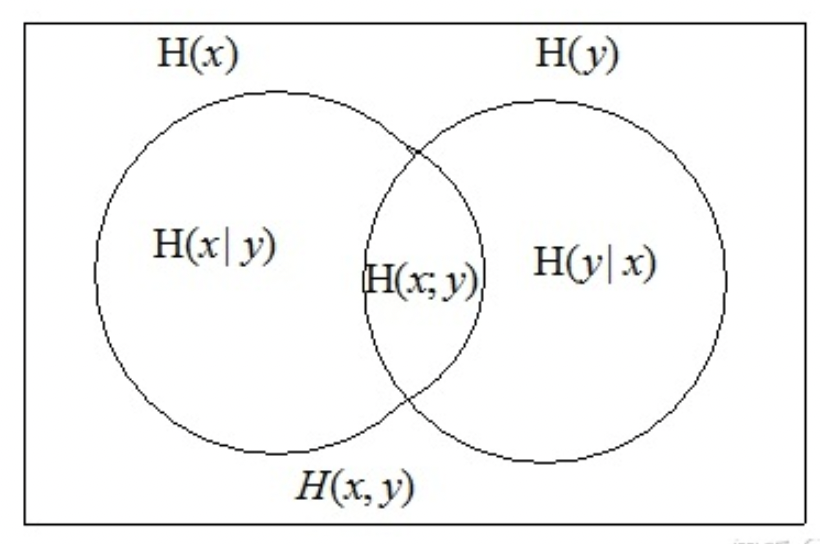
First, when we consider two event together, we can rewrite H(Y) as: \[ H(Y) = -\sum_i^m p(y=c_i)log(p(y=c_i) \\ = -\sum_j^n p(x = c_j)\sum_i^mp(y=c_i|x_=c_j)log(p(y=c_i)) \\ = \sum_x\sum_yp(x,y)log(p(y)) \]

\[ MI = H(x,y) - H(x|y) - H(y|x) = \sum_x\sum_yp(x,y)log\frac{p(x,y)}{p(x)p(y)} \]

\[ IG = H(y)-H(y|x) = \sum_x\sum_yp(x,y)log(p(y)) - \sum_x\sum_yp(x,y)log(p(y|x)) = MI \]

MI is usually mentioned when calculating the correlation of two variable, IG is mentioned when calculating the impurity reduction of one variable when splitting another variable

3. Entrophy measure for two distribution

3.1 KL Divergence(Relative Entrophy)

The KL divergence is the expectation(under true distribution) of the difference between information amount under predicted and true distribution \[ D_{KL}(p||q) = \sum_{i=1}^mp(y_i)\log(\frac{p(y_i)}{q(y_i)}) \] Where:

• q is the estimated distribution of y
• p is the real distribution of y

it can be used to evaluate an estimation of a distribution with the real distribution given

3.2 Cross Entrophy

The equation KL divergence can be written as: \[ D_{KL}(p||q) = \sum_{i=1}^mp(y_i)\log(\frac{p(y_i)}{q(y_i)}) = -\sum_i^mp(y_i)log(q(y_i)) - (-\sum_i^mp(y_i)log(p(y_i))) \] Obviously, the second term of this equation is \(H_p(x)\), which is the entrophy of the real data. In a machine learning problem, since real entrophy is fixed for a dataset, we can only minimize the first term. we call this term Cross entropy: \[ CH(p,q) = D_ {KL}(p||q) + H_p(X) = -\sum_i^mp(y_i)log(q(y_i)) \]